Tecnologia e Sistemi di Accordatura p.7
14 March 2012 Filed in: Personal
| Tuning
Theory
TECNOLOGIA E SISTEMI DI ACCORDATURA
Risorse hardware, software e online per la musica microtonale
(tesi di laurea di secondo livello in musica e nuove tecnologie - INDICE)
12tET etc.
Le considerazioni che hanno portato nel corso della storia alla costruzione di scale musicali sono state molto varie, da quelle numerologiche di Pitagora a quelle che ritengono che gli intervalli di una scala dovrebbero riflettere i rapporti degli armonici di un suono con forma d’onda periodica e, quindi, essere basati su semplici rapporti numerici (come nelle scale naturali o just intonation), fino a considerazioni pratiche che hanno portato al temperamento equabile.
Le tabelle che seguono mostrano la differenza tra 2 scale a 12 toni, una “just intonation” e quella equabile. Nella prima le differenze sono espresse come rapporto tra la fondamentale e ognuno dei gradi della scala.

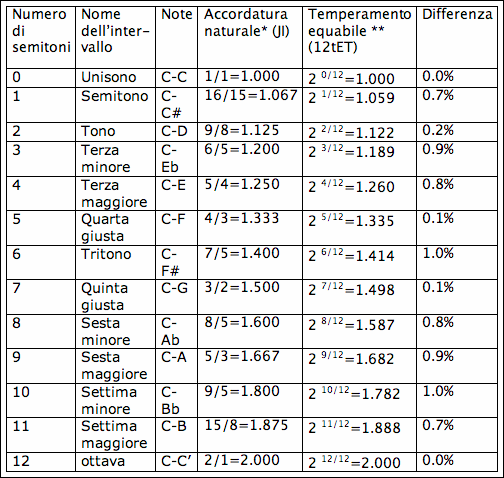
Le stesse 2 scale con i valori espressi in cents:

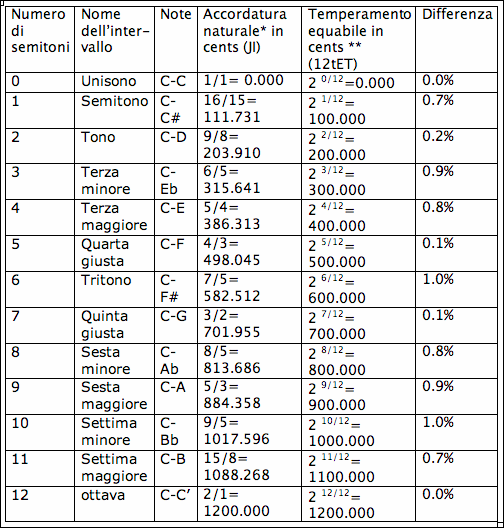
* questa tabella mostra una delle possibili varianti di accordatura naturale.
** La nostra percezione dell’altezza di un suono è logaritmica. Un’ottava corrisponde ad un raddoppio della frequenza. La divisione equabile dell’ottava in un qualsiasi numero di parti richiede che il rapporto tra ogni grado di essa e il successivo sia costante e nel caso del 12tET questo equivale alla radice dodicesima di due, ovvero quel numero che moltiplicato per sè stesso 12 volte dà come risultato 2 (
I seguenti esempi audio sono basati sulle 2 scale qui sopra:
Ascolta
01) scala di Do maggiore JI
02) scala di Do maggiore 12tET
03) scala di Do maggiore JI+12tET
04) intervallo di terza maggiore JI
05) intervallo di terza maggiore 12tET
06) intervallo di terza maggiore JI+12tET
07) intervallo di terza minore JI
08) intervallo di terza minore 12tET
09) intervallo di terza minore JI+12tET
10) intervallo di quinta giusta JI
11) intervallo di quinta giusta 12tET
12) intervallo di quinta giusta JI+12tET
13) accordo di Do maggiore JI
14) accordo di Do maggiore 12tET
15) accordo di Do maggiore JI+12tET
16) accordo di Do minore JI
17) accordo di Do minore 12tET
18) accordo di Do minore JI+12tET
Ma perché proprio 12 note? La risposta sta nel seguente grafico preso da questo sito :

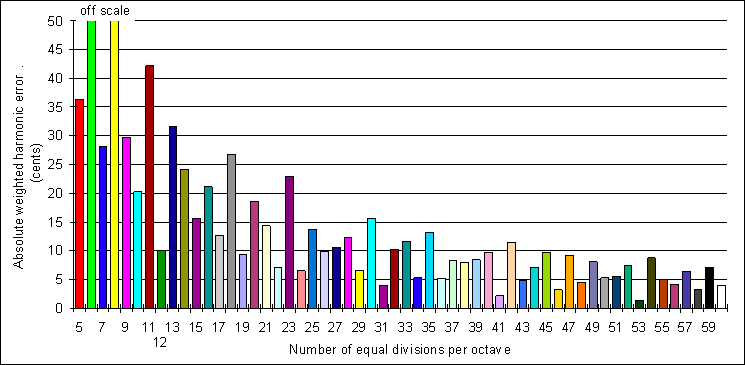
Il grafico mostra che 12tET è la scala equabile che col minor numero di gradi consente la migliore approssimazione a rapporti armonici (come in Just Intonation). Per ottenere risultati migliori bisogna arrivare a 19tET (teorizzata da Zarlino e Mersenne), a 22tET (molto simile al sistema d’accordatura utilizzato nella musica indiana) e oltre. Quindi 12tET è il compromesso migliore tra correttezza armonica e numero di note per ottava. Questo ci porta ad un’altra domanda:
Ma è proprio obbligatorio che una scala si ripeta nell’ambito di un’ottava? La risposta è NO, ovviamente! Un esempio comune è l’accordatura di un pianoforte durante la quale l’accordatore tende ad allargare l’estensione delle ottave, soprattutto di quelle estreme, per controbilanciare la normale inarmonicità delle corde, ovvero l’impossibilità, dovuta alla rigidità della corda, di produrre armoniche esatte.
Utilizzare una accordatura allargata con un timbro dai parziali perfettamente armonici, come è possibile negli strumenti elettronici, introduce dei battimenti che danno al timbro uno “scintillio” che, nella giusta dose, è molto gradevole, rendendolo meno statico e cangiante. Ovviamente questa sarebbe una ricetta indigesta per i fautori della “just intonation” che invece prediligono la statica bellezza di intervalli caratterizzati da semplici rapporti numerici.
A proposito di ottave allargate vorrei citare una scala inventata da X.J.Scott e da lui battezzata “superpythagorean” che grazie ad un’ottava leggermente allargata risolve il millenario problema del comma pitagorico. Come è noto, una scala pitagorica è basata su un circolo di quinte (3/2 ovvero 701.955 cents) con l’unico problema che dopo 12 di queste quinte (trasposte nella stessa ottava) non si torna al punto di partenza ma ad un altezza (in termini di suono) 23.5 cents distante dal punto di partenza. Questa distanza è appunto chiamata “comma pitagorico”.
Il ragionamento di Scott è il seguente: 12 quinte sovrapposte equivalgono a 7 ottave per cui 701,955 x 12 = 8.423,46 e 8.423,46 ÷ 7 = 1.203,35142857 cents, ovvero l’ampiezza di una pseudo-ottava che consente di avere una scala equabile di 12 gradi nella quale si crea un vero circolo di quinte giuste (3/2) e non una “spirale” di quinte come accade con un’ottava di 1200 cents.
In questa scala ogni grado dista dal successivo 100.279 cents.
Il moltiplicatore costante di questa scala è la radice dodicesima di 2.00387495941 (o detto in altri termini, la radice settima di 3/2).
La distanza dalla tonica, in cents, dei vari gradi è la seguente:
0., 100.279, 200.559, 300.838, 401.117, 501.396, 601.676, 701.955, 802.234, 902.513, 1002.793, 1103.072.
Un geniale utilizzo dell’ottava allargata!
Versione per internet - 2012
CARLO SERAFINI

Questo opera è distribuita con licenza Creative Commons Attribuzione - Non commerciale - Non opere derivate 3.0.

